Calculateur de Triangle

Résolvez vos Problèmes de Géométrie et d’Architecture en Ligne.

Exemples de calcul

Cas de calcul Résultat
Aire d'un triangle de base 10 cm et hauteur 7 cm 35 cm²
Théorème de Pythagore : hypoténuse d'un triangle rectangle (côtés 3 et 4) 5
Calcul d'un angle via la loi des sinus Résolution complète des angles internes

Comment utiliser le calculateur de triangle ?

Saisissez au moins trois valeurs connues (par exemple deux côtés et un angle, ou trois côtés). Le calculateur utilise le Théorème de Pythagore et la Loi des Sinus pour déduire toutes les autres mesures : aire, périmètre, angles manquants et hauteurs. Choisissez le type de triangle si vous le connaissez (rectangle, isocèle) pour accélérer la saisie.

Comment fonctionne le calculateur ?

Le calculateur résout les propriétés du triangle en fonction des données fournies. S’il s’agit d’un triangle rectangle, il utilise la relation a² + b² = c². Pour les triangles quelconques, il applique la formule de Héron pour l’aire. En France, ces calculs sont fondamentaux pour l’architecture paysagère ou les devoirs de mathématiques du collège. Imaginez calculer l’aire d’un massif de fleurs triangulaire dans un jardin public : avec des côtés de 4m, 5m et 6m, l’outil vous donne précisément la surface pour acheter le bon nombre de plants.Diagramme du Triangle Rectangle

Conseils d’Experts 💡

  • Saisissez les côtés ou angles connus avec précision.
  • Sélectionnez le type de triangle si requis pour le calcul.

📋Étapes de calcul

  1. Entrez les côtés ou angles connus.

  2. Sélectionnez le type de triangle si nécessaire.

  3. Cliquez sur "Calculer" pour trouver l’aire et les valeurs manquantes.

Erreurs à éviter ⚠️

  1. Saisir des longueurs de côtés qui ne peuvent pas former un triangle réel.
  2. Confondre la base et la hauteur dans les triangles qui ne sont pas rectangles.
  3. Tenter d'utiliser le théorème de Pythagore sur des triangles non rectangles.
  4. Ne pas vérifier que la somme des angles internes est exactement de 180 degrés.

Applications pratiques📊

  1. Calculez l’aire pour les devoirs de géométrie ou les projets de conception.

  2. Associez avec notre convertisseur de surface pour les ajustements d’unités.

  3. Explorez différents types de triangles pour la pratique éducative.

Questions Fréquentes (FAQ)

Que signifie un calculateur de triangle ?

Dans son sens le plus général, un solveur de triangle est un calculateur qui calcule l’aire, les longueurs des côtés et les angles de n’importe quel triangle à partir d’une mesure unique. Par exemple, avec le calculateur d’angles de CalcMate, entrez les valeurs des trois longueurs de côtés du triangle. Le calculateur utilisera plusieurs formules, comme la formule de Héron pour l’aire ou les relations trigonométriques pour les angles, pour donner des triangles droits, scalènes ou isocèles avec précision.

Comment déterminer l’aire d’un triangle ?

Si vous connaissez la base et la hauteur, utilisez (Base * Hauteur) / 2. Si vous ne connaissez que les côtés, le calculateur applique la Formule de Héron.

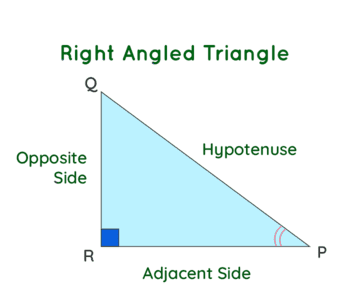
Comment utiliser un calculateur de triangle rectangle ?

Indiquez les deux côtés de l’angle droit. L’outil calculera l’hypoténuse instantanément grâce à Pythagore, ainsi que les angles de 30, 60 ou 45 degrés.

Comment trouver l’angle d’un triangle ?

En saisissant les trois côtés, le calculateur utilise la Loi des Cosinus pour extraire la mesure exacte de chaque angle en degrés.

Comment déterminer une mesure extérieure ?

En utilisant les relations trigonométriques (Sinus, Cosinus), l’outil peut déduire les longueurs extérieures à partir d’un angle et d’un côté adjacent.

Quelles formules sont utilisées dans le calculateur de triangle ?

Notre calculateur utilise plusieurs formules différentes, selon le type d’aire avec base et hauteur, il utilise (base × hauteur)/2 ; et pour trois côtés, il utilise la formule de Héron, A = √[s(s-a)(s-b)(s-c)], où s = (a+b+c)/2. Les autres côtés ou angles que nous ne fournissons pas seront calculés à l’aide de la loi des sinus et/ou des cosinus en fonction des entrées données. Ces processus ont été approuvés par la Mathematical Association of America (MAA).

Le calculateur de triangle peut-il prendre en charge les problèmes de géométrie 3D ?

Le calculateur de triangle est conçu pour les triangles 2D, résolvant les côtés, les angles ou l’aire. Pour la géométrie 3D (par exemple, les tétraèdres), utilisez les résultats 2D comme base pour d’autres calculs ou employez un logiciel spécialisé pour l’analyse volumétrique.

Que se passe-t-il si mes entrées de triangle sont invalides ?

Si les entrées violent les propriétés du triangle (par exemple, les longueurs des côtés ne respectent pas l’inégalité triangulaire : a + b > c), le calculateur affichera une erreur. Vérifiez les longueurs des côtés ou les angles (sommant à 180°) pour vous assurer qu’ils forment un triangle valide.

🔢Outils Recommandés

Calculateur d’Écart-Type
Calculateur de Matrices
Calculateur de Trigonométrie
Note : Ce calculateur est conçu pour fournir des estimations utiles à des fins d'information. Bien que nous fassions tout notre possible pour garantir l'exactitude, les résultats peuvent varier en fonction des lois locales et des circonstances individuelles. Nous vous recommandons de consulter un conseiller professionnel pour toute décision importante.