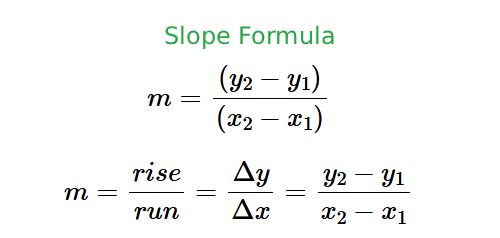Line Slope Calculator

Find the slope (m) of a line, also known as the gradient, using the coordinates of any two points on that line.

Was this calculator helpful?

★ ★ ★ ★ ★
4.7/5 (22 votes)

Calculation Examples

Calculation Case Result
Points (1, 2) and (3, 6) Slope (m) = 2
Points (-1, 5) and (2, -1) Slope (m) = -2
Angle of 45 degrees Slope (m) = 1

How to Use the Calculator?

Enter the coordinates of two points into the tool. The calculator computes the gradient ($m$) using the fundamental linear equation: $$m = \frac{y_2 - y_1}{x_2 - x_1}$$ Results are displayed instantly to help you analyze the steepness and direction of the line.Slope Formula

The Four Types of Slope (Positive, Negative, Zero, Undefined)

The slope (m) is a measure of the steepness and direction of a line, often described as "rise over run." There are four possible outcomes when calculating slope:

1. Positive Slope (m > 0): Line rises from left to right.

2. Negative Slope (m < 0): Line falls from left to right.

3. Zero Slope (m = 0): Horizontal line (\Delta y = 0).

4. Undefined Slope: Vertical line (\Delta x = 0).

The concept of slope is fundamental in algebra, geometry, and calculus, used to analyze rates of change in physics, engineering, and data trends.

Slope Formula Diagram

Useful Tips 💡

  • Always verify that the coordinates belong to the same line segment.
  • Remember that the slope value remains constant for any two points on a straight line.

📋Steps to Calculate

  1. Input x and y coordinates of two points.

  2. Verify input accuracy.

  3. Click "Calculate" to find the slope.

Mistakes to Avoid ⚠️

  1. Mixing up (x₁, y₁) and (x₂, y₂) - slope becomes negative of the correct value.
  2. Using rise/run instead of Δy/Δx when points are not ordered.
  3. Thinking vertical line has slope 0 - it’s undefined.
  4. Dividing by zero when points have same x-coordinate and not recognizing undefined slope.

Practical Applications📊

  1. Calculate for construction or landscaping projects.

  2. Pair with our Triangle Calculator for geometric analysis.

  3. Design drainage systems based on slope gradients.

Questions and Answers

What is a slope calculator?

A slope calculator is a geometry tool that determines the "steepness" or inclination of a line by calculating the vertical and horizontal distance between two specific points on a Cartesian plane. By inputting the $(x, y)$ coordinates, you receive the slope value, which represents the constant rate of change along that line. CalcMate’s tool offers quick, dependable outcomes for students, engineers, and designers who need to quantify the direction and magnitude of a linear path.

How to find slope with two points?

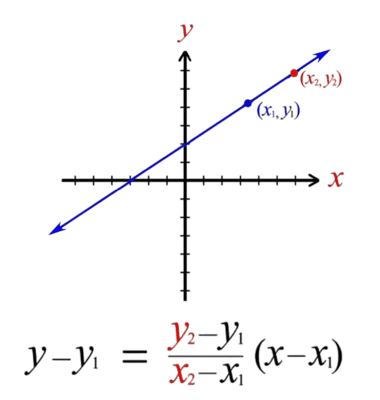
To find the gradient or slope, you must input the $(x, y)$ coordinates for two distinct points on the line. The tool applies the fundamental slope formula: $m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}$. This "rise over run" calculation reveals how much the $y$-value increases or decreases for every unit of horizontal movement along the $x$-axis, providing a precise numerical value for the line's orientation.

What is the slope of a line?

The slope of a line defines its steepness and direction. In coordinate geometry, it is the ratio of the "rise" (vertical change) to the "run" (horizontal change) between any two points. A positive slope indicates the line rises from left to right, while a negative slope indicates it falls. A slope of zero represents a perfectly horizontal line. Using our calculator allows you to obtain this value instantly without the risk of manual subtraction or division errors.

How to calculate slope from a table?

To calculate slope from a data table, simply pick any two pairs of coordinates $(x_1, y_1)$ and $(x_2, y_2)$ from the list. As long as the relationship is linear, any two points will yield the same result. Plug these coordinates into our point-slope form calculator, and the tool will compute the rate of change based on the provided data, which is especially useful for analyzing experimental results or financial trends.

Can I use a slope calculator for graphing?

Yes, determining the slope from two points is an essential step in graphing linear equations. It provides the "m" value in the slope-intercept form equation $y = mx + b$. Knowing the slope is necessary to correctly position the line on a graph and to understand its behavior. By inputting two known points, you can quickly find the slope needed to plot additional points or to identify the angle of the line relative to the axes.

Which formulas are used in Slope Calculator?

The calculator employs the standard slope formula: $m = \frac{y_2 - y_1}{x_2 - x_1}$, where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of two points on the line. This formula, derived from the principles of coordinate geometry, allows for the calculation of both steepness and direction. This methodology is universally accepted and endorsed by the National Council of Teachers of Mathematics (NCTM) for its pedagogical accuracy in defining linear functions.

Can this tool be used for practical applications?

Absolutely. Beyond the classroom, slope calculations are vital in construction for determining roof pitch and road grades to ensure proper drainage. In physics, the slope of a position-time graph represents velocity, while in financial analysis, it is used to quantify the rate of change in stock prices or economic indicators. This tool allows you to translate real-world inclination and data trends into actionable numerical values.

🔢Try More Calculators

Advanced Scientific Calculator
Triangle Calculator
Variance and Standard Deviation Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.