Remainder Calculator

Compute precise integer quotients and remainders. Our engine implements the Euclidean Division Theorem for consistent results across all integer sets.

Remainder: -
Quotient (integer): -
Quotient (decimal): -

Was this calculator helpful?

★ ★ ★ ★ ★
4.5/5 (17 votes)

Calculation Examples

Calculation Case Result
Remainder of 100 ÷ 7 2
Remainder of 25 ÷ 4 1
Remainder of 50 ÷ 8 2

How to Execute Division with Remainder

To obtain a precise result, enter the dividend and the divisor. Unlike standard decimal calculators, this tool executes integer division, returning both the quotient and the specific remainder. For instance, dividing $25$ by $7$ yields a quotient of $3$ and a remainder of $4$, expressed as $25 = 7 \times 3 + 4$.

The Euclidean Division Algorithm

This calculator is built on the Division Theorem. For any two integers $a$ (dividend) and $b$ (divisor, $b \neq 0$), there exist unique integers $q$ (quotient) and $r$ (remainder) such that: $a = b \times q + r$ and $0 \le r < |b|$. Our implementation ensures $r$ is always non-negative, following the Euclidean definition.Mathematical representation of remainder division

Useful Tips 💡

  • A remainder of 0 indicates that the divisor is a factor of the dividend.
  • The remainder is mathematically constrained to be strictly less than the divisor.
  • Our tool uses the Euclidean method, ensuring the remainder is always positive for consistent results.

📋Steps to Calculate

  1. Identify the dividend (numerator) and the divisor (denominator).

  2. Input integers into the fields (supports negative and large values).

  3. Analyze the output to distinguish between the integer quotient and the residual remainder.

Mistakes to Avoid ⚠️

  1. Divisor of Zero: Division by zero is undefined in all algebraic systems and will return an error.
  2. Inputting Decimals: This tool is optimized for Integer Arithmetic; for decimals, standard division is more appropriate.
  3. Modulo vs. Remainder: Be aware that some programming languages (like C++ or Java) handle negative remainders differently than the Euclidean standard used here.

Advanced Practical Applications📊

  1. Algorithm Verification: Test modulo (%) logic for software development and cyclic data structures.

  2. Number Theory: Solve problems related to congruence relations and modular arithmetic.

  3. Cryptography: Verify integer partitions and shifts in basic encryption algorithms.

  4. Education: Validate long division steps and the Remainder Theorem for polynomial preparation.

Questions and Answers

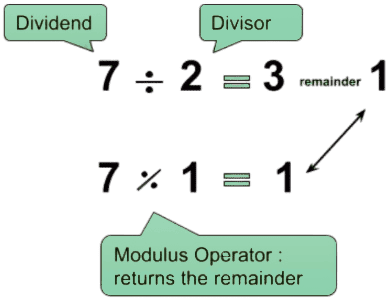
What is the difference between a Remainder and a Modulo operation?

While often used interchangeably, the difference lies in how they handle negative dividends. A "remainder" (standard division) can be negative in many programming languages. However, the Modulo operation ($a \pmod n$) usually follows the Floored or Euclidean definition, ensuring the result is always non-negative ($0 \le r < n$). Our calculator defaults to the Euclidean standard for mathematical consistency.

What is the mathematical formula for the Remainder Theorem?

The tool operates based on the Division Algorithm theorem: $$a = b \times q + r$$ where $a$ is the dividend, $b$ is the divisor, $q$ is the integer quotient, and $r$ is the remainder. For a result to be a true Euclidean remainder, it must satisfy the condition $0 \le r < |b|$.

How does this tool handle extremely large numbers (BigInt)?

Standard calculators often fail at 16 digits due to 64-bit float limitations. Our engine utilizes Arbitrary-Precision Arithmetic (BigInt), allowing you to find the remainder for numbers with hundreds of digits. This is particularly useful for cryptographic verification and checksum algorithms like CRC-32 or Luhn.

Why is the Modulo operator critical in computer programming?

The modulo operator (usually `%` or `mod`) is a cornerstone of logic in software development. It is used for cyclic patterns (e.g., repeating a sequence every $n$ elements), determining parity (if $n \% 2 = 0$, the number is even), and hashing, where data is mapped to specific slots in a fixed-size table.

How can I convert a decimal result back to a whole remainder?

If a basic calculator shows $10 / 4 = 2.5$, the $.5$ is the fractional part. To find the integer remainder $r$: take the decimal part ($0.5$) and multiply it by the original divisor ($4$). Result: $0.5 \times 4 = 2$. Thus, the remainder is $2$.

What are the applications of Modulo in Cryptography?

Modulo arithmetic is the "engine" of Public Key Cryptography (RSA). It allows for Modular Exponentiation, where a number is raised to a power and then reduced by a large prime modulus. This creates "one-way" functions that are easy to compute but extremely difficult to reverse without a private key.

Does this calculator support the "Chinese Remainder Theorem" logic?

This tool finds the remainder for a single division. However, it provides the precise $r$ values needed as inputs for the Chinese Remainder Theorem (CRT), which is used to solve systems of simultaneous congruences in advanced number theory and parallel computing.

🔢Try More Calculators

Hex Calculator
Multiplication Calculator & Solver
Circumference Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.