Rest-Rechner

Quotienten und Rest jeder ganzzahligen Division sofort berechnen, auch für große und negative Zahlen.

Rest: -
Quotient (ganzzahlig): -
Quotient (dezimal): -

War dieser Rechner hilfreich?

★ ★ ★ ★ ★
4.7/5 (25 Stimmen)

Berechnungsbeispiele

Berechnungsfall Ergebnis
100 ÷ 7 (100 mod 7) Quotient 14, Rest 2
45 ÷ 4 Quotient 11, Rest 1 (45 = 4 × 11 + 1)
-17 ÷ 5 (euklidisch) Quotient -4, Rest 3 (-17 = 5 × (-4) + 3)

Wie benutzt man den Rest-Rechner?

Geben Sie den Dividenden (die zu teilende Zahl) in das erste Feld und den Divisor (die Zahl, durch die geteilt wird) in das zweite Feld ein. Das Tool unterstützt positive und negative ganze Zahlen sowie sehr große Zahlen. Nach dem Klick auf „Berechnen" erscheinen sofort der ganzzahlige Quotient und der Rest.

Für 25 ÷ 7 zeigt der Rechner Quotient 3 und Rest 4, weil 25 = 7 × 3 + 4 gilt. Das ist ideal für Schüler, die Hausaufgaben zur schriftlichen Division überprüfen, oder für Programmierer, die Modulo-Logik testen, beispielsweise um zu prüfen, ob eine Zahl gerade ist (Rest bei Division durch 2 gleich 0) oder um Wochentage aus Datumsangaben zu berechnen.

Wie funktioniert die Restberechnung?

Der Rechner verwendet den euklidischen Divisionsalgorithmus: für zwei ganze Zahlen a (Dividend) und b (Divisor, b ≠ 0) existieren eindeutige ganze Zahlen q (Quotient) und r (Rest), sodass \(a = b \times q + r\) mit \(0 \leq r < |b|\) gilt. Der Rest ist nach dieser Definition stets nicht-negativ, auch bei negativem Dividenden. Für -17 ÷ 5 ergibt das q = -4 und r = 3, weil -17 = 5 × (-4) + 3. Diese euklidische Konvention unterscheidet sich von der truncated-Division mancher Programmiersprachen (z. B. C), bei der negative Reste möglich sind.Rest-Rechner Beispiel: 25 geteilt durch 7 ergibt Quotient 3 und Rest 4

Nützliche Tipps 💡

  • Der Rest ist immer kleiner als der absolute Betrag des Divisors. Für ÷ 7 liegt der Rest stets zwischen 0 und 6.
  • Ist der Rest 0, ist der Dividend durch den Divisor ohne Rest teilbar. Das lässt sich so schnell prüfen wie bei einer Primzahlsuche.
  • Für negative Dividenden verwendet dieser Rechner die euklidische Definition: der Rest bleibt stets positiv oder null. Das entspricht dem Verhalten von Python (%-Operator) und Mathematica, aber nicht von C oder Java, die truncated Division verwenden.

📋Schritte zur Berechnung

  1. Dividenden eingeben (die Zahl, die geteilt werden soll).

  2. Divisor eingeben (die Zahl, durch die geteilt wird; darf nicht null sein).

  3. Auf „Berechnen" klicken: ganzzahliger Quotient und Rest erscheinen sofort.

Häufige Fehler ⚠️

  1. Null als Divisor eingeben: Division durch null ist mathematisch nicht definiert und liefert kein Ergebnis.
  2. Dividend und Divisor vertauschen: 17 ÷ 5 (Rest 2) und 5 ÷ 17 (Rest 5) sind völlig verschiedene Operationen.
  3. Dezimalzahlen eingeben: der Divisionsalgorithmus ist nur für ganze Zahlen definiert; Dezimalwerte wie 7,5 als Divisor liefern kein ganzzahliges Ergebnis.

Praktische Anwendungen📊

  1. Hausaufgaben zur schriftlichen Division mit Rest kontrollieren und Rechenwege nachvollziehen.

  2. Modulo-Operationen in der Programmierung und Kryptographie durchführen, z. B. für Hash-Funktionen oder Schaltjahr-Prüfungen.

  3. Zeiteinheiten umrechnen, zum Beispiel 200 Minuten: 200 ÷ 60 = Quotient 3 (Stunden), Rest 20 (Minuten).

  4. Teilbarkeit großer Zahlen prüfen, ohne einen vollständigen Divisionsalgorithmus manuell durchführen zu müssen.

Fragen und Antworten

Was ist ein Rest bei der Division?

Der Rest ist die ganze Zahl, die nach einer ganzzahligen Division übrig bleibt. Teilt man 17 durch 5, passt 5 genau dreimal in 17 (5 × 3 = 15), und der Rest ist 17 - 15 = 2. Formal gilt nach dem euklidischen Divisionsalgorithmus: für Dividend a und Divisor b existieren eindeutige ganze Zahlen q und r mit a = b × q + r und 0 ≤ r < |b|. Der Rest ist per Definition stets nicht-negativ.

Wie funktioniert ein Modulo-Rechner?

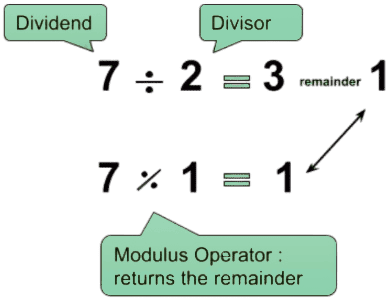
Ein Modulo-Rechner berechnet den Rest einer ganzzahligen Division. Für 10 mod 3 gilt: 3 passt dreimal in 10 (3 × 3 = 9), Rest = 10 - 9 = 1. In der Programmierung steht dafür meist das %-Symbol (Python, Java, C). Typische Anwendungen: Prüfung auf geradzahligkeit (n mod 2 = 0), Wochentag-Berechnung aus Tagesnummer (Tagesnummer mod 7) oder zyklische Indizierung in Arrays.

Ist der Rest immer positiv?

Bei der euklidischen Division, die dieser Rechner verwendet, ist der Rest immer nicht-negativ (0 oder größer). Für -17 ÷ 5 ergibt das nach euklidischer Definition Quotient -4 und Rest 3, weil -17 = 5 × (-4) + 3 und 3 ≥ 0. Manche Programmiersprachen wie C und Java verwenden stattdessen truncated Division: dort wäre der Rest -2 (weil -17 = 5 × (-3) + (-2)). Dieser Rechner folgt der mathematisch standardisierten euklidischen Definition.

Warum diesen Rechner statt eines Standard-Taschenrechners nutzen?

Ein Standard-Taschenrechner liefert für 10 ÷ 3 das Dezimalergebnis 3,333... Ein Rest-Rechner gibt stattdessen Quotient 3 und Rest 1 aus, weil 10 = 3 × 3 + 1. Für Schulaufgaben zur schriftlichen Division, für Modulo-Logik in der Programmierung und für Teilbarkeitsbeweise ist das ganzzahlige Ergebnis zwingend erforderlich. Außerdem unterstützt dieser Rechner sehr große Zahlen, die die Kapazität gängiger Taschenrechner überschreiten.

Welche Formel wird zur Restberechnung verwendet?

Der Rechner verwendet den euklidischen Divisionsalgorithmus: \(a = b \times q + r\) mit \(0 \leq r < |b|\), wobei a der Dividend, b der Divisor, q der ganzzahlige Quotient und r der Rest ist. Der Quotient ergibt sich als \(q = \lfloor a / b \rfloor\) (Abrunden auf die nächste ganze Zahl), der Rest als \(r = a - b \times q\). Für a = 25, b = 7: q = 3, r = 25 - 7 × 3 = 4.

Kann ich sehr große Zahlen dividieren?

Ja. Der Rechner verarbeitet sehr große ganze Zahlen, die die Kapazität herkömmlicher Taschenrechner überschreiten. Die Berechnung erfolgt intern mit beliebig großer Ganzzahlarithmetik, sodass auch mehrstellige Zahlen präzise Ergebnisse liefern, ohne Rundungsfehler durch Gleitkommadarstellung.

🔢Weitere Rechner Ausprobieren

Hex-Rechner
Multiplikationsrechner
Umfangsberechner
Hinweis: Dieser Rechner dient dazu, hilfreiche Schätzungen zu Informationszwecken bereitzustellen. Obwohl wir uns um Genauigkeit bemühen, können die Ergebnisse je nach örtlichen Gesetzen und individuellen Umständen variieren. Wir empfehlen, bei wichtigen Entscheidungen einen professionellen Berater zu Rate zu ziehen.